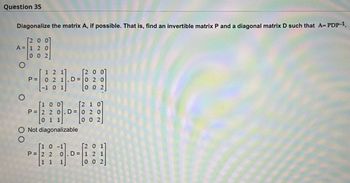
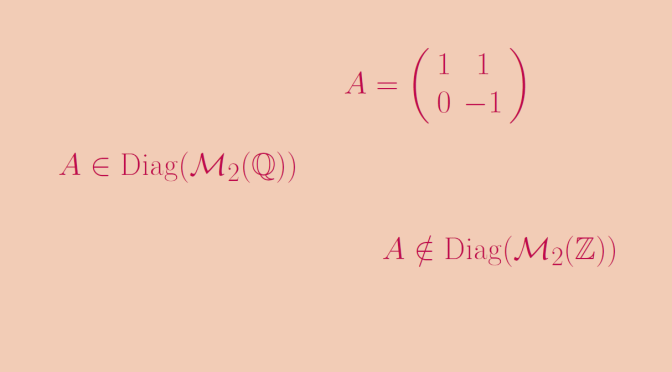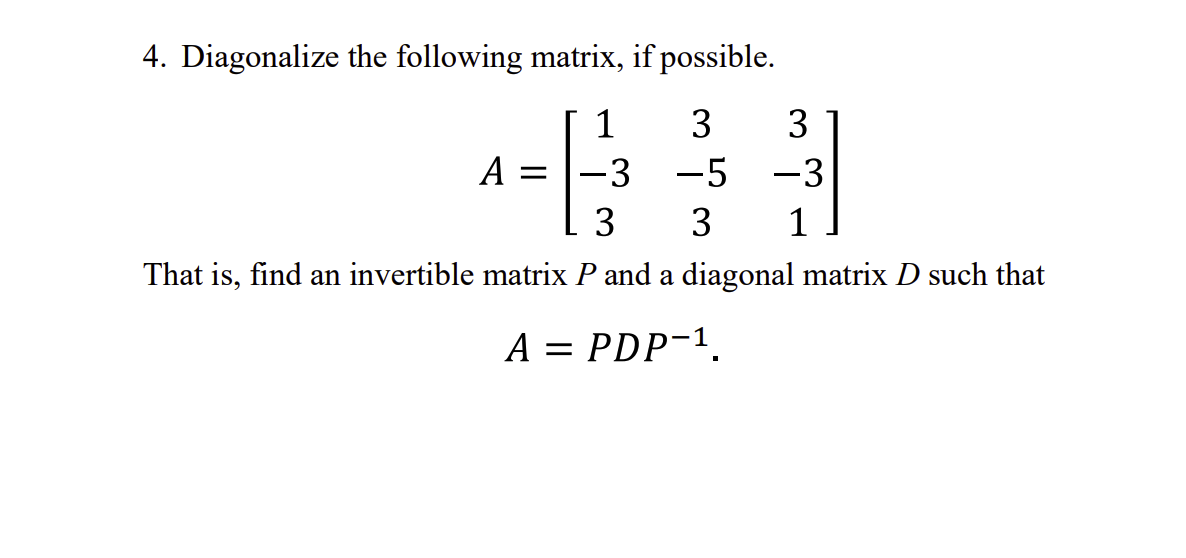SOLVED: Diagonalize the matrix A, if possible: That is, find an invertible matrix P and a diagonal matrix D such that A= PDP-1 A = -10 -11 P = Ho-[ -3 dv-[::9 4 [ -3 H D
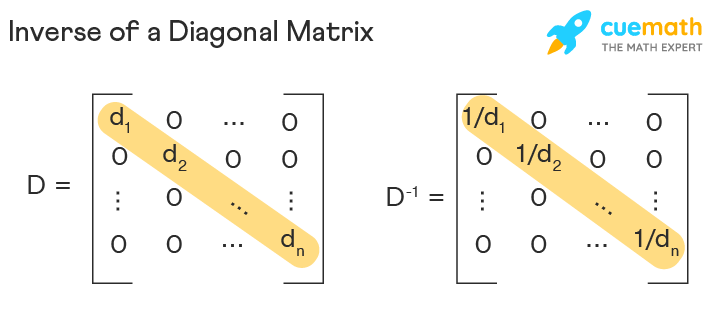
linear algebra - Proof for why symmetric matrices are only orthogonally diagonalizable - Mathematics Stack Exchange
A diagonalizable matrix over Q but not over Z | Math Counterexamples
SOLVED: Diagonalize the following matrix; if possible. 2 A = The eigenvalues are 5 and 4 (one of them is repeted). If the matrix is not diagonal- izable, explain, why nOl If
Solved Diagonalize the matrix A, if possible. That is, find | Chegg.com
SOLVED: Diagonalize the matrix A, if possible. That is,find an invertible matrix P and a diagonal matrix D such that A= PDP-1 A = -
Solved Diagonalize the matrix A, if possible. That is, find | Chegg.com
Solved Diagonalize the matrix A, if possible. That is find | Chegg.com
Diagonalizable matrix - Wikipedia
Inverse of Diagonal Matrix - Formula, Proof, Examples
Example of Diagonalizing a 2 x 2 Matrix - YouTube
Solved Diagonalize the matrix A, if possible. That is, find | Chegg.com
Not diagonalizable - YouTube
SOLVED: Question 8 (20 points) Diagonalize the matrix (That is, find a diagonal matrix D and an invertible matrix P such that A = PDP-I (Do not find the inverse of P)
Are non symmetric matrices Diagonalizable? - Quora
Answered: Diagonalize the matrix A, if possible.… | bartleby
Solved 4. Diagonalize the following matrix, if possible. = 1 | Chegg.com
Determine whether A is diagonalizable and, if so, find an in | Quizlet
SOLVED: Diagonalize the matrix A, if possible: That is, find an invertible matrix P and a diagonal matrix D such that A= PDP-1 8) A = -5 -8 A) P-l? H-[i8 P-l;
True or False. Every Diagonalizable Matrix is Invertible | Problems in Mathematics
Answered: Diagonalize the matrix A, if possible.… | bartleby
Eigenvalues and Eigenvectors - ppt video online download
Solved Diagonalize the matrix A, if possible. That is, find | Chegg.com
